Time Frequency Duality

An particularly interesting characteristic of Fourier transforms is time-frequency duality. This duality exposes a beautiful deep symmetry between the time and frequency domains of a signal.

For example, a sinusoid in the time domain is an impulse in the frequency domain, and vice versa.

Here's what a 1-second 20hz sine wave looks like. If you play this on your audio device, you'll hear a 20hz tone.

	import numpy as np
	import matplotlib.pyplot as plt
	# Generate Sine wave
	hz = 20
	x = np.arange(0, 1, 0.001) # 1 second
	y = np.sin(2 * np.pi * hz * x)
	plt.figure(figsize=(10, 3))
	plt.plot(x, y)
	plt.show()

view raw sine-wave.py hosted with ❤ by GitHub

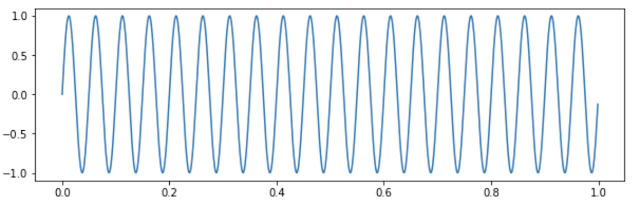20hz Sine Wave

When you take the Fourier transform of the wave, and plot the frequency domain representation of the signal, you get an impulse in the bin representing the 20hz. (Ignore the tiny neighbours for now.)

	# Generate an integer-period sine wave to
	# eliminate spectral leak.
	hz = 20
	x = np.linspace(0, 2 * np.pi * hz, 128 * hz)
	y = np.sin(x)
	plt.figure(figsize=(10, 3))
	plt.plot(x, y)
	plt.show()
	# We're only interested in the real components
	fft_y = fft.rfft(y) / (len(x) / 2)
	plt.figure(figsize=(10, 3))
	plt.bar(np.arange(100), np.absolute(fft_y)[:100]) # Show just the first 100 bins
	plt.show()

view raw sine-wave-fft.py hosted with ❤ by GitHub

Frequency Domain of 20hz Sine Wave

If you play this transformed representation out to your audio device, you'll hear a click, generated from the single impulse pushing the speaker's diaphragm. This is effectively an impulse signal.

Okay, let's create an impulse signal by hand -- a string of zeros, with a 1 somewhere in the middle. Play this on your speaker, and, again, you'll hear a click. This signal is no different from the the previous transformed signal, except for maybe the position of the impulse.

	points = 256
	y = np.zeros(points, dtype="complex64")
	y[20] = np.complex(1,0) # stick a 1 into the 20th position
	plt.figure(figsize=(10, 3))
	plt.bar(np.arange(100), np.absolute(y)[:100]) # Show the first 100 points
	plt.show()

view raw impulse-signal.py hosted with ❤ by GitHub

So, check this out. If you take the the FFT of the impulse and plot the frequency domain representation, you get... a sinusoid!

	points = 256
	y = np.zeros(points, dtype="complex64")
	y[20] = np.complex(1,0)
	ifft_y = fft.irfft(y) * points
	plt.figure(figsize=(10, 3))
	plt.plot(ifft_y)
	plt.show()

view raw impulse-fft.py hosted with ❤ by GitHub

This works both ways. You can the the inverse FFT of a sine wave in the frequency domain, to produce an impulse in the time domain.

	x = np.linspace(0, 2 * np.pi * hz, points * hz)
	y = np.sin(x)
	plt.figure(figsize=(10, 3))
	plt.bar(np.arange(75), y[:75 * 10:10]) # sample every 10th element for bar graph
	plt.show()
	fft_y = fft.ifft(y.astype("complex64")) * 2
	plt.figure(figsize=(10, 3))
	plt.bar(np.arange(100), np.absolute(fft_y[:100]))
	plt.show()

view raw impulse-fft-inverse.py hosted with ❤ by GitHub

Inverse Fourier Transform of a Sine Wave

This is a wonderfully striking phenomenon, which I think reveals a lot about our perception of nature.

For example, here's another property of time-frequency duality -- convolutions in the time domain are multiplications in the frequency domain, and vice versa. Because multiplications require far fewer operations than convolutions, it's much simpler to operate on frequency domain representations of signals.

Your inner ear consists of lots of tiny hairs that vary in thickness and resonate at different frequencies sending frequency domain representations of sound to your brain -- i.e., your ear evolved a little DSP chip in it to make it easier on your brain.